2021/01/13
かけ算の話

健康診断に向けてアップを始めたいと思っている今日この頃です。
今回は弊社の荒川が「かけ算の話」をしました。
今日はかけ算の話をしようと思います。
初めに、小学校で習う標準的な筆算から見ていきましょう。
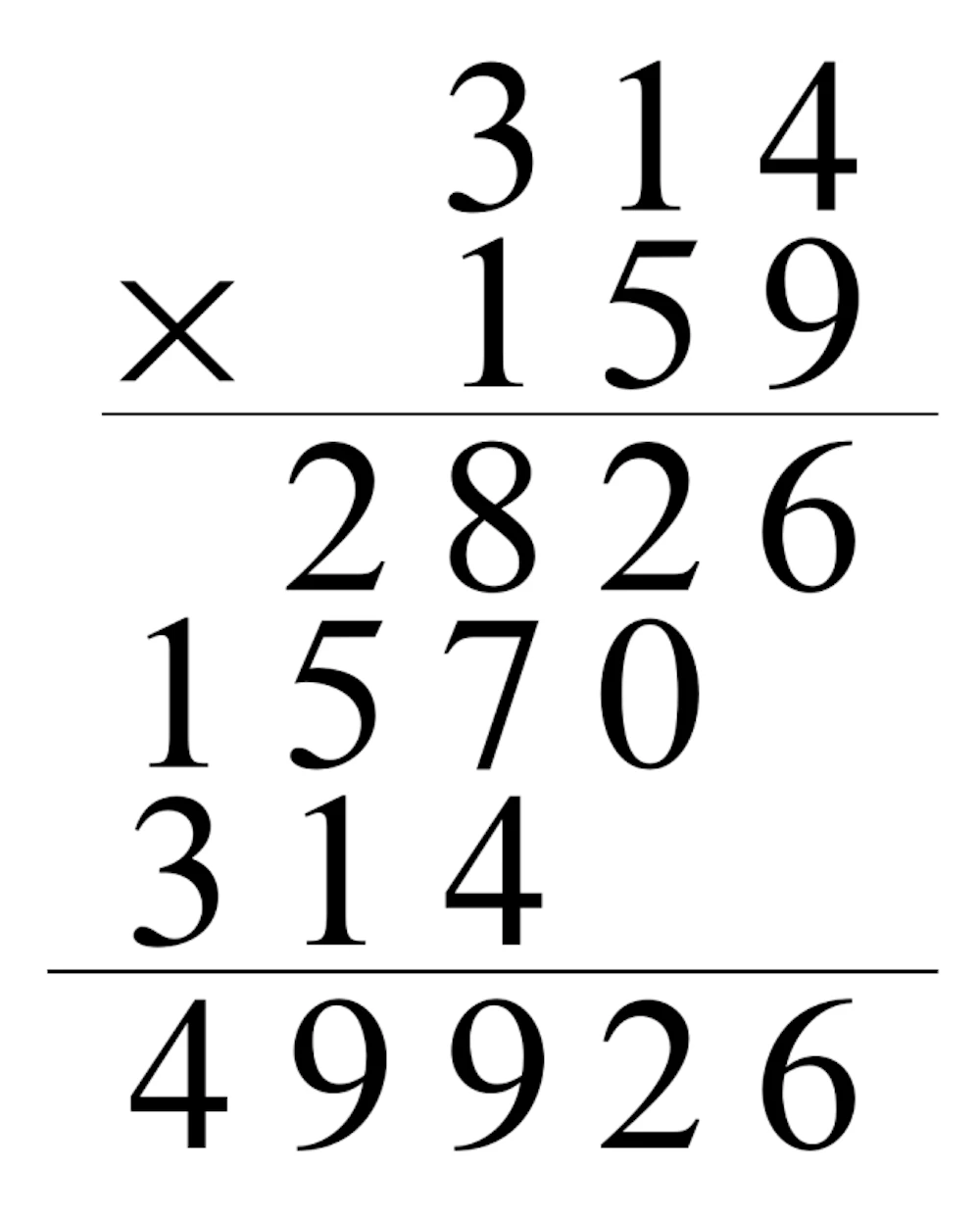
このような二つの数を掛ける筆算があったとすると、一桁ずつ下の数と上の数を計算していくと思いますが、この筆算のアルゴリズムが何のオーダーかを考えた時、三桁の数を各数字ごとに3回ずつ計算するので合計9回計算が行われます。
二番目の数の各桁毎に最初の数の各桁を順次掛け合わせて、繰り上がりを処理しつつ途中結果を書きます。次にそれらをシフトしながら足し合わせて最終的な答えを得ます。
シフト演算と足し算はかけ算に比べて無視できるほど処理が速いので、全体として 0(n^2) の計算複雑度になります。
筆算とはこういうやり方なわけです。
これはKaratsuba法と呼ばれており、何故誰も考えつかなかったのかというぐらい簡単な方法です。
例として、10進数で4桁同士のかけ算をすることを考えてみましょう。
この時、いきなりかけ算をするのではなく、4桁の数字を上の2桁と下の2桁の二つに分解して考えます。
xとyという4桁の数字があった場合、式で書くと
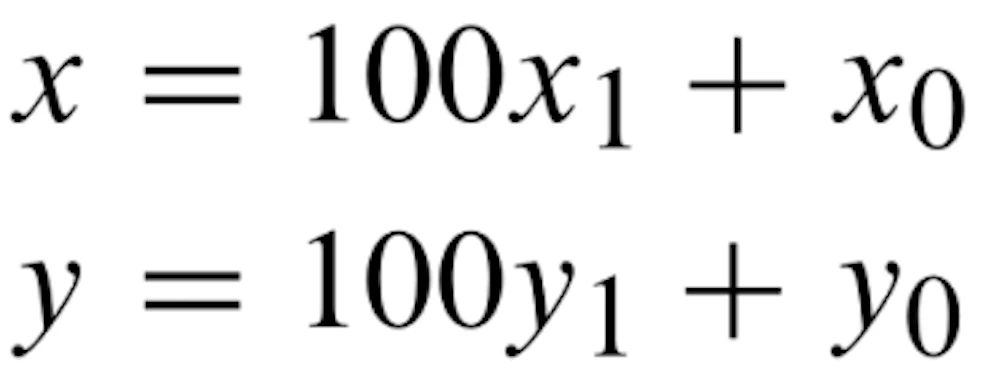
というふうにそれぞれ書けます。
これをかけ算してみましょう。
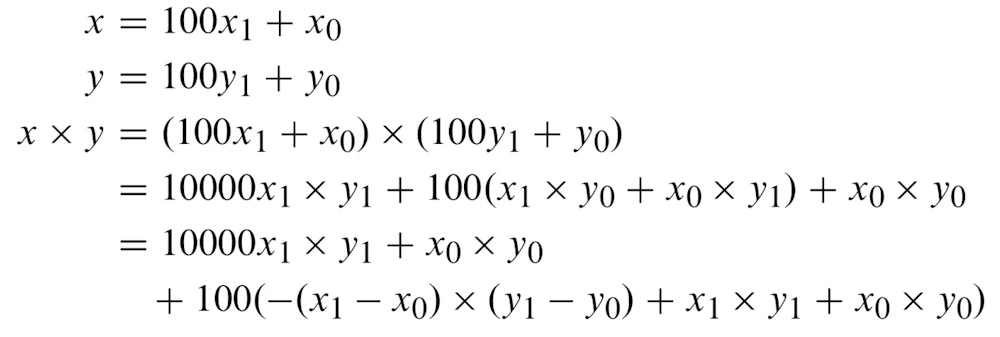
目的としてかけ算の数を減らしたいわけですが、一番下の式は一見5つ、かけ算があるように見えますが、よく見てみると一つの式の中に同じ式が重複していることがわかると思います。既に計算されている式は計算する必要がないので、そうするとなんとかけ算が3回で済むのです。
理解できると信じられないぐらい簡単な方法だということがわかるのですが、Anatoly Karatsuba が出てくるまで誰も考えつきませんでした。
数学者たちはこれを受けてすぐに Karatsuba法の改良に取りかかります。
このアルゴリズムをより効率的にしたものが広く使われており、例えば GNU Multiple Precision Arithmetic Library の核としても使われています。
ただし、このライブラリでも対象の数が数千桁よりも小さい場合は、 Karatsuba 法を含む他のアルゴリズムを使った方が速く計算できるので使い分けられています。
簡単な例として、635×258 を実行することを考えてみましょう。
突然なのですが、まず初めにそれぞれの数を係数に持つ多項式を導入します。導入する意味についてはおいおいわかってきます。
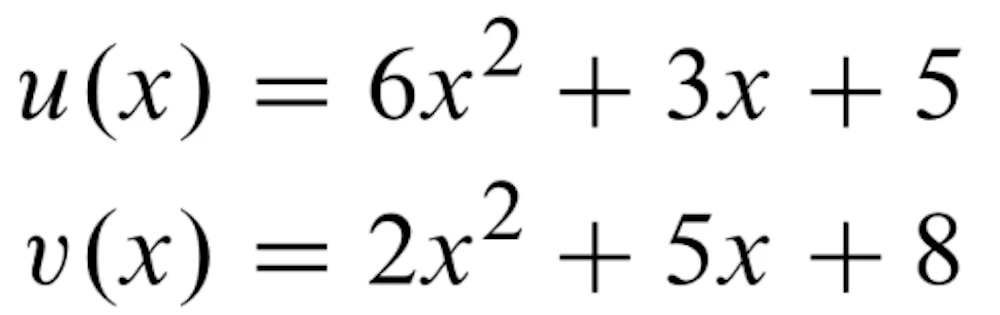
これをかけ算すると、
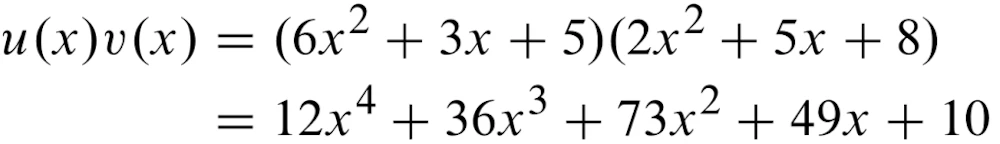
このような式が成り立ちますが、例えば x = 10 としてみると、もとの 635×258 が再現されることが分かります。その結果は 163830 となりますが、これでは多項式をただ展開しただけで高速化には全く関係がありません。
しかし、結果が 4 次の多項式になるということは最初から分かっていますから、多項式を展開するのではなくて、4 次の方程式の係数を未知数として解けば結果が得られるはずです。つまりちょっとズルができるのです。
u(x)v(x)は 4 次の多項式、
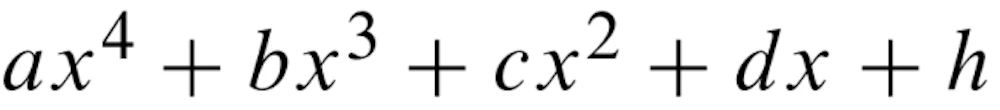
となりますから、未知数が5つあると考えると、5 組の連立方程式を解けば結果は求まるはずです。
例えば x として 0,1,2,3,4 を選ぶと、
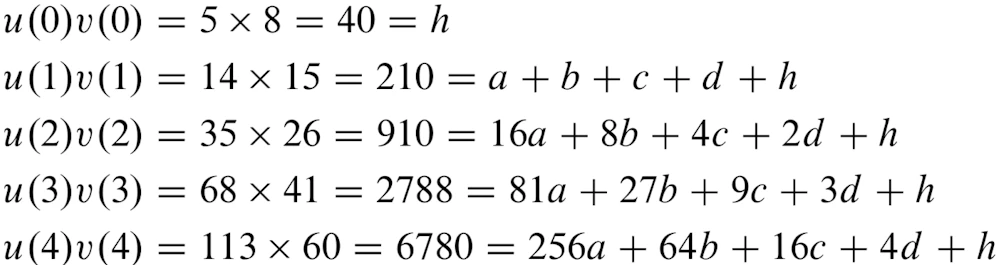
式の展開をしなくてもこれを解けば答えが求められます。
ですがこのままではまだ速く計算することはできません。
というのも x に適当に選んだ数を使っているからです。5 つの x をどのように選ぶかが重要になってきます。
それではどのような数を入れれば良いかですが、答えを言ってしまうと、 1 の 5乗根を入れるのが正解です。
1 の 5 乗根とは、5 回かけて 1 になる数です。実数の範囲では、5 回かけて 1 になる数は 1 しかありませんが、範囲を複素数に広げると全部で 5 つの答えがあります。
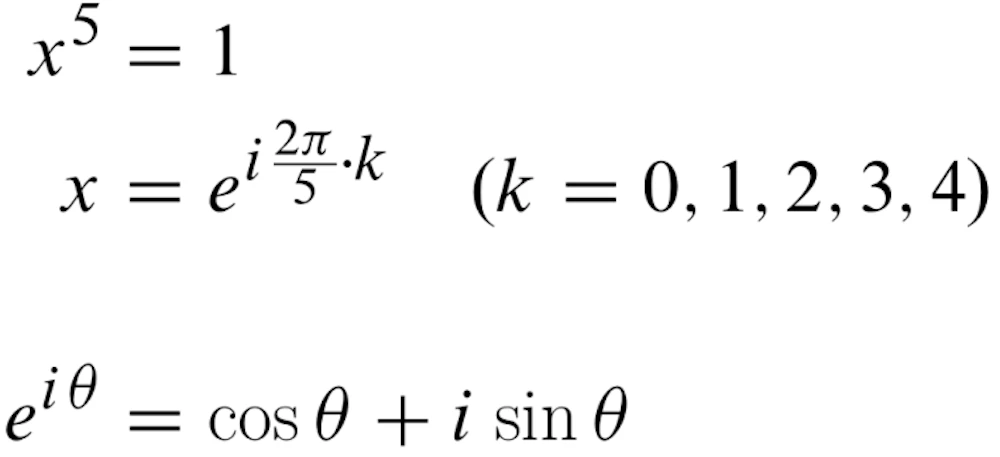
このxをu(x)とv(x)に代入するとミラクルが起こります。
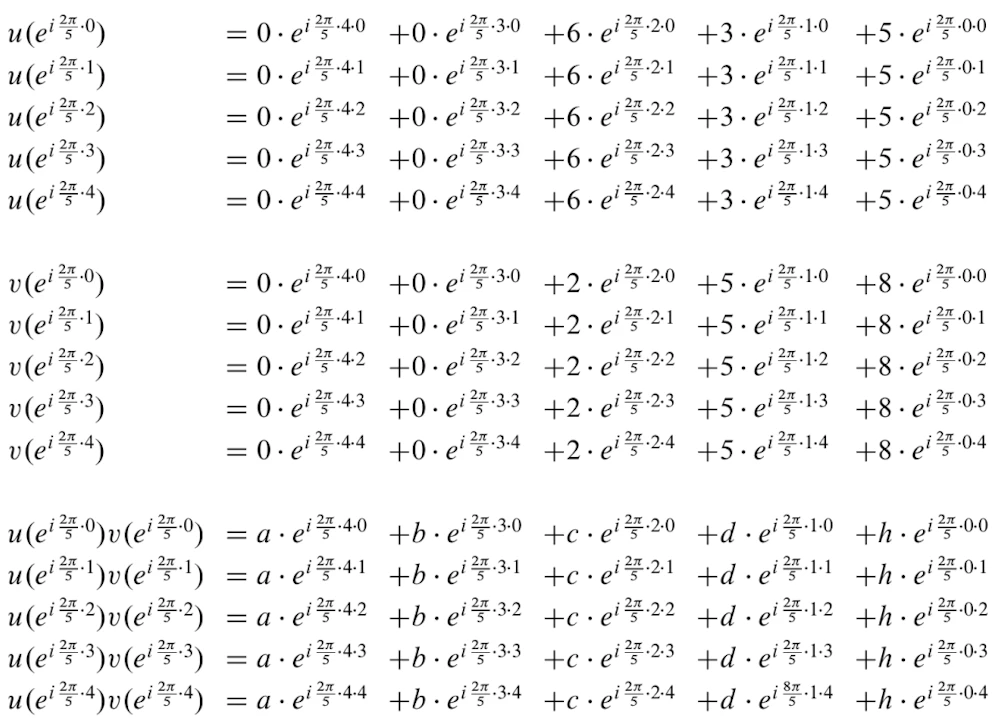
これらの計算式は、実は(離散)フーリエ変換と呼ばれる式そのものなのです。フーリエ変換は、時間変化する信号波形があった時にその周波数成分を計算する演算のことです。
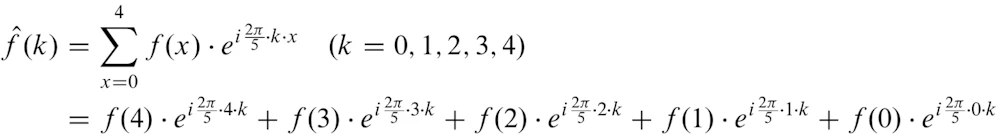
従ってこれらは FFT(Fast Fourie Transform)という速いアルゴリズムを使えば n log n のステップで計算することが可能です。
数値の多項式への変換により洗練された手法を使うことで Schönhage と Strassen は最終的なかけ算のステップ数として O(n log n log(log n)) を得ました。
しかし、かけ算という基本的な演算のステップ数にしては log が多く複雑すぎるということで、多くの人が美的観点からかけ算のステップ数は最終的に O(n log n) であるべきだと考えました。ですがこの発見から30年以上、これ以上に速い方法を誰も思いつかなかったのです。
実用的な応用には不向きな方法ではあったのですが、その理論的な進展は Joris van der Hoeven と David Harvey の二人に衝撃を与えました。彼らは5年間に渡って Furer の上限をさらに改良する10篇余りの論文を執筆します。
その結果、2019年3月、ついに log(log n) 項を完全に消去する方法が編み出されました。
FFTというのは対象の数が 2 の幕乗になっている時が一番速いのですが、サンプリングポイントをわざと増やして 2 の幕乗になるようにエ夫し、それに高次元バージョンの FFT を組み合わせるようにしたことがキーでした。
このアルゴリズムではスピードと精度のバランスを取るため、FFT に現れる複素数の切り捨て操作を行う必要があります。厳密な整数のかけ算を行うために、複素数の多項式の近似的な計算を行い、最後に元に戻って厳密な値が得られるのです。
この O(n log n) はHarvey と van der Hoeven のアルゴリズムがSchonhage Strassenや Furer 等他のどんな既知のアルゴリズムよりも速いことを示していますが、ただし n は十分に大きな値である必要があります。
「十分に大きな」はとてつもない値であり、 nのビット数が
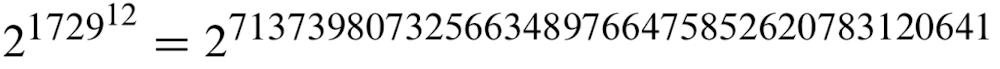
よりも大きくなる場合です。ちなみに観測可能な全宇宙の素粒子の数が "たった" 2^702 個と見積もられていることからもこの桁数がいかに膨大なものかが分かると思います
Harveyとvan der Hoeven はアルゴリズムをこれ以上最適化しませんでした。というのも理論的な興味からn log nの係数には興味が沸かなかったというのが一つ、アルゴリズムを評価する計算で 1729 という数字が現れたからというのがもう一つの理由です。
あとで説明しますが、1729 という数字は数学者にとって特別な数字なのです。
現在のところ実用的な応用は限られますが、理論的な影響は途方もなく大きいと言われています。というのも乗算はあらゆる数学的な操作の中心にあるものだからです。なので、その速度は計算複雑性理論においては、 物理学における光速に匹敵するほど重要なわけです。
かけ算が O(n log n) ステップで実行できることは示されましたが、これよりも速いアルゴリズムが存在しないことは (多くの人はそう考えていますが) 今のところまだ証明されていません。
Ramanujan は数学を専門的に学んでいないからか証明の必要性が理解できなかったそうです。そこでHardy は Ramanujan が朝持ってくる成果を一日かけて証明するというような研究スタイルを取り、その結果、大きな成果を得ました。
しかし、Ramanujan は敬虔なヒンドゥー教徒で厳格なベジタリアンだったこともあり、イギリスの生活が合わず次第に衰弱していきます。最終的にインドに帰国するもののまもなく1920年に亡くなってしまいました。
Ramanujan は本当の天才でした。彼がどれだけ並外れていたのか説明することは難しいですが、彼の考えた式をいくつか紹介します。
最初の式は恒等式です。
とんでもない数の項が出てくる式なのですが、それが右辺できれいに二乗の形にまとまっています。Hardy と Ramanujan はこの式を使って右辺が常に正または 0 であることから重要な不等式を証明しています。
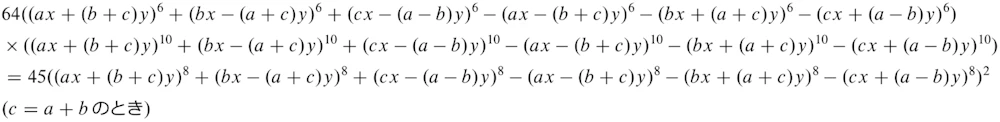
続いてはインドの不思議な旋律と呼ばれる公式です。
左側は連分数と言って、ある数を分数で次々と近似していく時に出てくる式です。これが右辺のような形にまとまるとはただただ驚くしかありません。
何故こんな式が考えだせるのかわかりませんが、この式もちゃんと成り立っています。
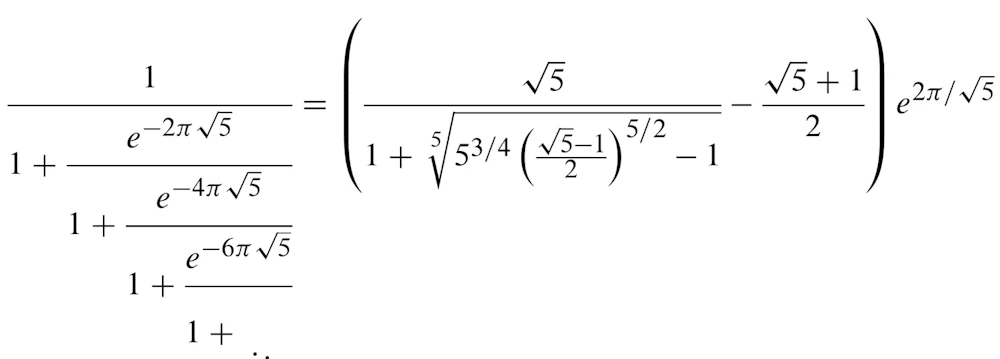
それでは 1729 の話をします。
ある日、療養所に入院していた Ramanujan を Hardy が見舞いに訪れました。その時に「乗ってきたタクシーのナンバーが 1729 だったが、特に特徴のない数だったよ」という話を Hardy が話したことに端を発します。
これに対して Ramanujan は「いえ 先生。1729 はとても興味深い数です。それは二つの整数の 3 乗の和として二通りに表すことができる最小の自然数です」というのをたちどころに返したそうです。
式にするとこういうことです。
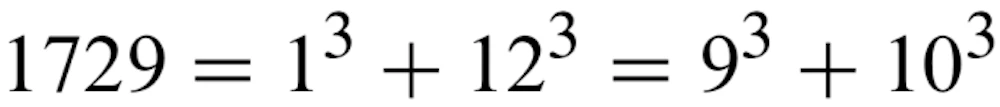
このエピソードから 1729 は数学者に「タクシー数」として親しまれるようになりました。
今日の話の参考文献を紹介しておきますので、興味のある方は読んでみてください。Ramanujan については映画にもなっているのでよかったら見てみてください。
Multiplication hits the speed limit.
DOl:https://doi.org/10.1145/3371387
Harvey, D. and van der Hoeven, J.
Integer Multiplication in Time O(n log n).
Knuth, D.E.
The Art of Computer Programming, vol. 2: Seminumerical Algorithms, 3rd edn, Addison-Wesley, 1998, 294-318.
映画「奇蹟がくれた数式」(The Man Who Knew Infinity)
今回は弊社の荒川が「かけ算の話」をしました。
今日はかけ算の話をしようと思います。
初めに、小学校で習う標準的な筆算から見ていきましょう。
筆算のアルゴリズムのステップ数
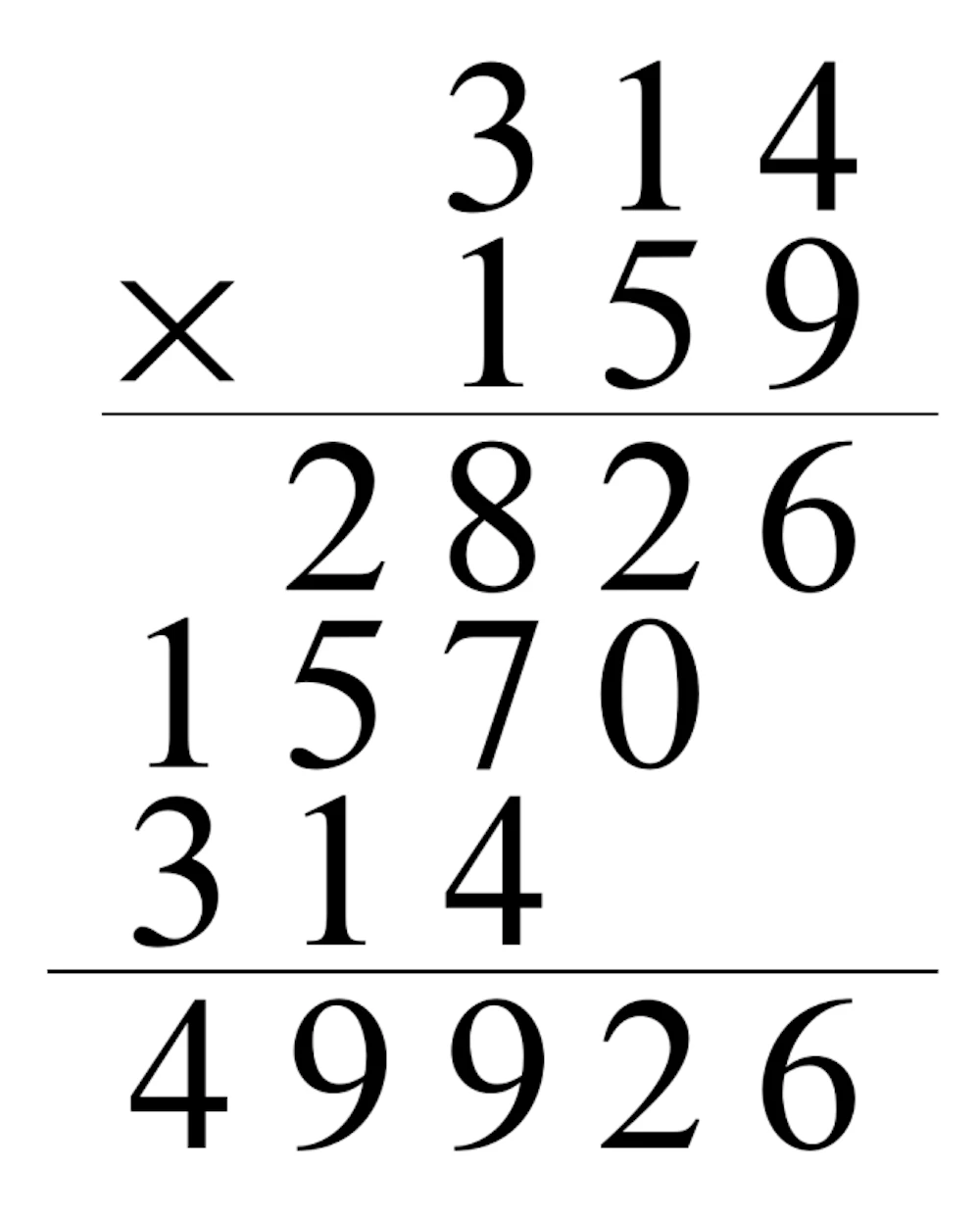
このような二つの数を掛ける筆算があったとすると、一桁ずつ下の数と上の数を計算していくと思いますが、この筆算のアルゴリズムが何のオーダーかを考えた時、三桁の数を各数字ごとに3回ずつ計算するので合計9回計算が行われます。
二番目の数の各桁毎に最初の数の各桁を順次掛け合わせて、繰り上がりを処理しつつ途中結果を書きます。次にそれらをシフトしながら足し合わせて最終的な答えを得ます。
シフト演算と足し算はかけ算に比べて無視できるほど処理が速いので、全体として 0(n^2) の計算複雑度になります。
筆算とはこういうやり方なわけです。
Karatsuba法
人類は何千年もの間、この単純な方法よりも速いかけ算の方法を誰も知りませんでした。ところが、1960年に Andrey Kolmogorov (20世紀を代表する数学者の一人)がモスクワ州立大学のセミナーで、「乗算に n^2 ステップより少ないアルゴリズムは存在しないことを証明せよ」という問題を出した時に、Anatoly Karatsuba(当時23歳の学生) という数学者が n^1.58 ステップしか要しない方法を考え出し、逆にアルゴリズムが存在することを証明しました。これはKaratsuba法と呼ばれており、何故誰も考えつかなかったのかというぐらい簡単な方法です。
例として、10進数で4桁同士のかけ算をすることを考えてみましょう。
この時、いきなりかけ算をするのではなく、4桁の数字を上の2桁と下の2桁の二つに分解して考えます。
xとyという4桁の数字があった場合、式で書くと
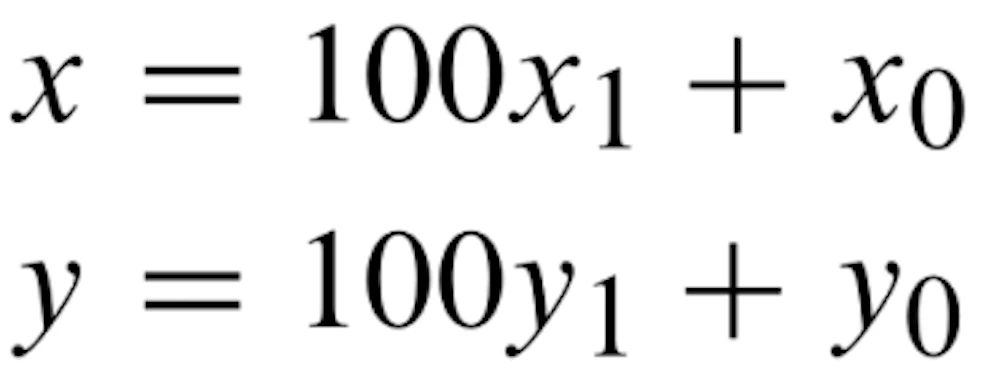
というふうにそれぞれ書けます。
これをかけ算してみましょう。
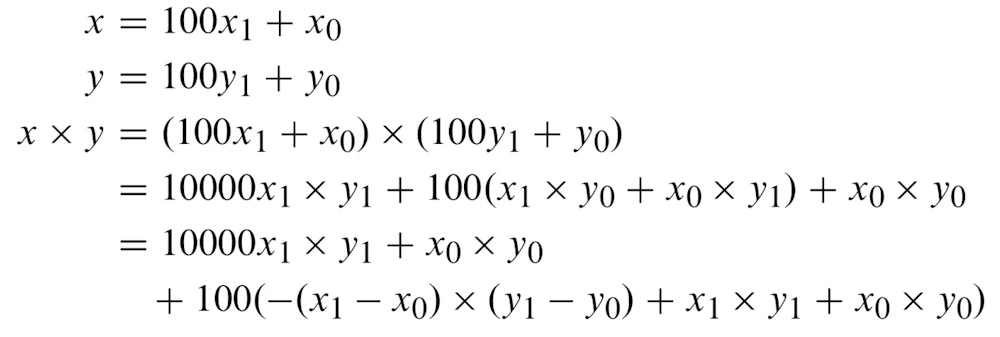
目的としてかけ算の数を減らしたいわけですが、一番下の式は一見5つ、かけ算があるように見えますが、よく見てみると一つの式の中に同じ式が重複していることがわかると思います。既に計算されている式は計算する必要がないので、そうするとなんとかけ算が3回で済むのです。
理解できると信じられないぐらい簡単な方法だということがわかるのですが、Anatoly Karatsuba が出てくるまで誰も考えつきませんでした。
数学者たちはこれを受けてすぐに Karatsuba法の改良に取りかかります。
Schönhage Strassen 法
そして1971年、Arnold Schönhage と Volker Strassen という数学者がようやく n^1.58 よりも遥かに効率の良い n log n log(log n) のアルゴリズムを考え出しました。このアルゴリズムをより効率的にしたものが広く使われており、例えば GNU Multiple Precision Arithmetic Library の核としても使われています。
GNU Multiple Precision Arithmetic Library
GNU Multi-Precision Library(GMP)は、多倍長整数など任意精度の算術ライブラリで、フリーソフトウェアである。符号付き整数、有理数、浮動小数点数を扱う。
Wikipedia:GNU Multiple Precision Arithmetic Library
ただし、このライブラリでも対象の数が数千桁よりも小さい場合は、 Karatsuba 法を含む他のアルゴリズムを使った方が速く計算できるので使い分けられています。
簡単な例として、635×258 を実行することを考えてみましょう。
突然なのですが、まず初めにそれぞれの数を係数に持つ多項式を導入します。導入する意味についてはおいおいわかってきます。
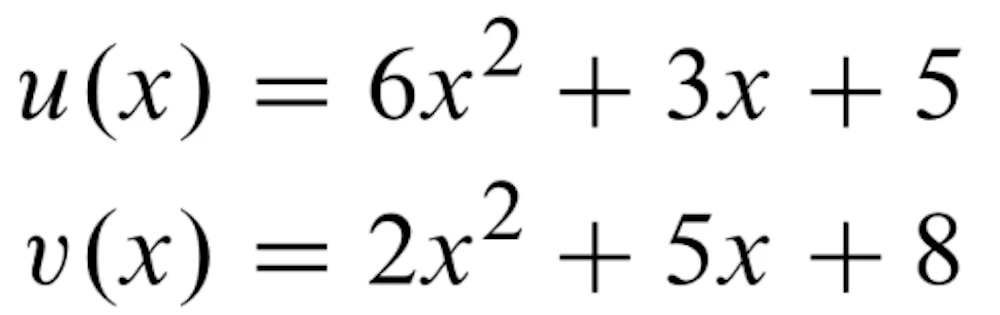
これをかけ算すると、
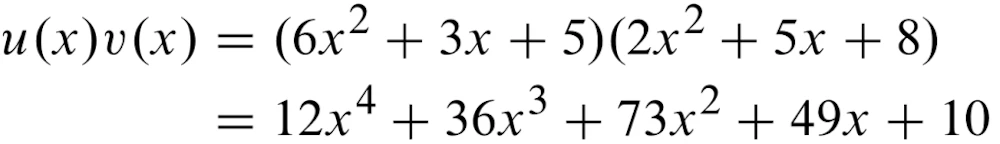
このような式が成り立ちますが、例えば x = 10 としてみると、もとの 635×258 が再現されることが分かります。その結果は 163830 となりますが、これでは多項式をただ展開しただけで高速化には全く関係がありません。
しかし、結果が 4 次の多項式になるということは最初から分かっていますから、多項式を展開するのではなくて、4 次の方程式の係数を未知数として解けば結果が得られるはずです。つまりちょっとズルができるのです。
u(x)v(x)は 4 次の多項式、
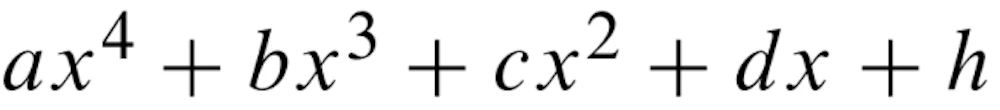
となりますから、未知数が5つあると考えると、5 組の連立方程式を解けば結果は求まるはずです。
例えば x として 0,1,2,3,4 を選ぶと、
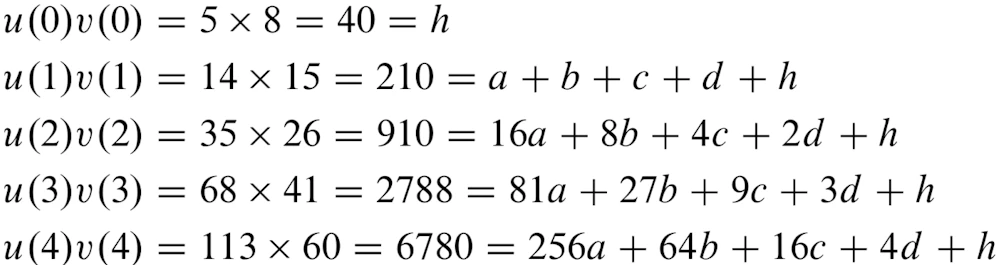
式の展開をしなくてもこれを解けば答えが求められます。
ですがこのままではまだ速く計算することはできません。
というのも x に適当に選んだ数を使っているからです。5 つの x をどのように選ぶかが重要になってきます。
それではどのような数を入れれば良いかですが、答えを言ってしまうと、 1 の 5乗根を入れるのが正解です。
1 の 5 乗根とは、5 回かけて 1 になる数です。実数の範囲では、5 回かけて 1 になる数は 1 しかありませんが、範囲を複素数に広げると全部で 5 つの答えがあります。
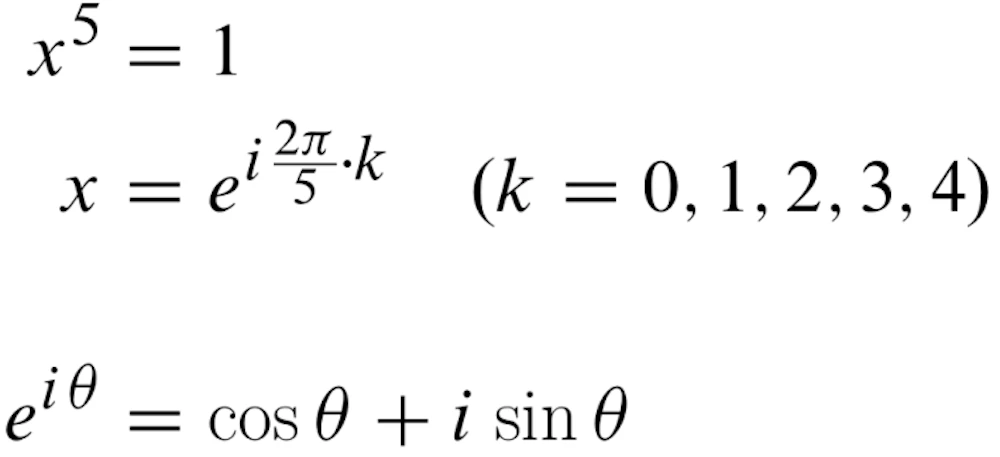
このxをu(x)とv(x)に代入するとミラクルが起こります。
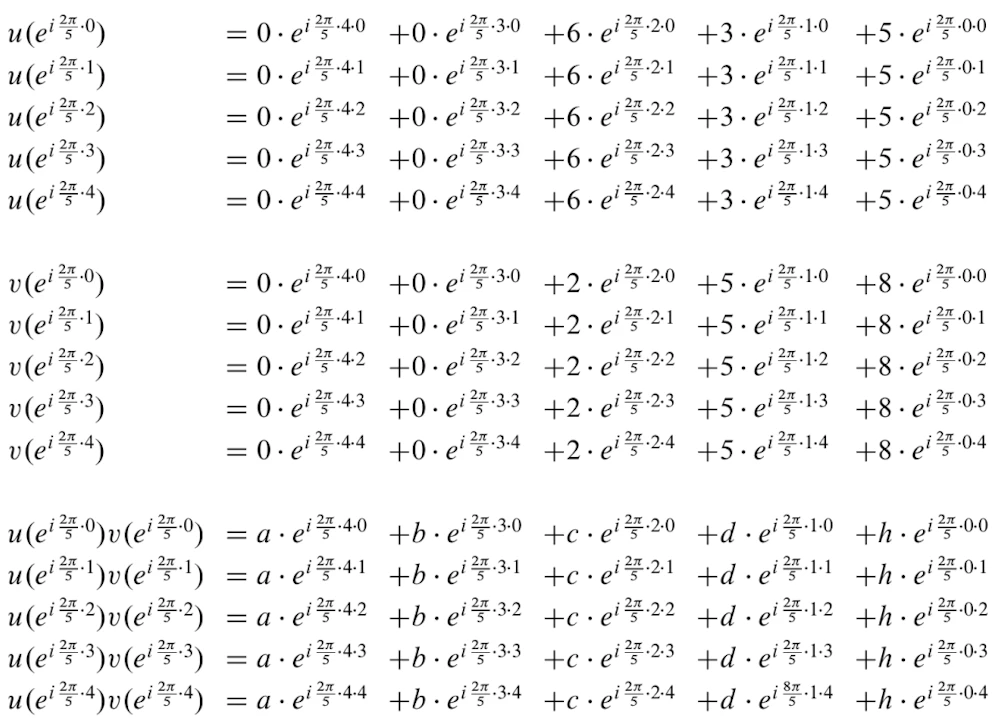
これらの計算式は、実は(離散)フーリエ変換と呼ばれる式そのものなのです。フーリエ変換は、時間変化する信号波形があった時にその周波数成分を計算する演算のことです。
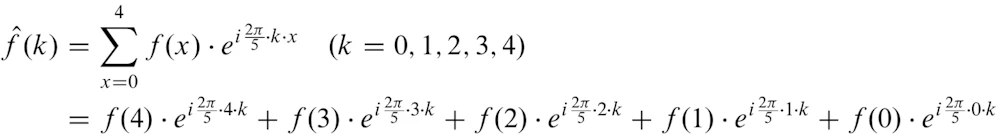
従ってこれらは FFT(Fast Fourie Transform)という速いアルゴリズムを使えば n log n のステップで計算することが可能です。
数値の多項式への変換により洗練された手法を使うことで Schönhage と Strassen は最終的なかけ算のステップ数として O(n log n log(log n)) を得ました。
しかし、かけ算という基本的な演算のステップ数にしては log が多く複雑すぎるということで、多くの人が美的観点からかけ算のステップ数は最終的に O(n log n) であるべきだと考えました。ですがこの発見から30年以上、これ以上に速い方法を誰も思いつかなかったのです。
最終的な解決へ
2007年になって、Martin Furer がついに log(log n) の項をやや小さな値に置き換えることに成功しました。実用的な応用には不向きな方法ではあったのですが、その理論的な進展は Joris van der Hoeven と David Harvey の二人に衝撃を与えました。彼らは5年間に渡って Furer の上限をさらに改良する10篇余りの論文を執筆します。
その結果、2019年3月、ついに log(log n) 項を完全に消去する方法が編み出されました。
FFTというのは対象の数が 2 の幕乗になっている時が一番速いのですが、サンプリングポイントをわざと増やして 2 の幕乗になるようにエ夫し、それに高次元バージョンの FFT を組み合わせるようにしたことがキーでした。
このアルゴリズムではスピードと精度のバランスを取るため、FFT に現れる複素数の切り捨て操作を行う必要があります。厳密な整数のかけ算を行うために、複素数の多項式の近似的な計算を行い、最後に元に戻って厳密な値が得られるのです。
この O(n log n) はHarvey と van der Hoeven のアルゴリズムがSchonhage Strassenや Furer 等他のどんな既知のアルゴリズムよりも速いことを示していますが、ただし n は十分に大きな値である必要があります。
「十分に大きな」はとてつもない値であり、 nのビット数が
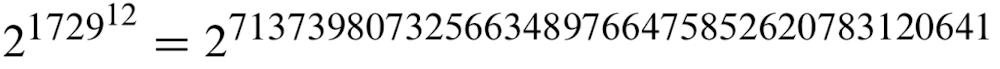
よりも大きくなる場合です。ちなみに観測可能な全宇宙の素粒子の数が "たった" 2^702 個と見積もられていることからもこの桁数がいかに膨大なものかが分かると思います
Harveyとvan der Hoeven はアルゴリズムをこれ以上最適化しませんでした。というのも理論的な興味からn log nの係数には興味が沸かなかったというのが一つ、アルゴリズムを評価する計算で 1729 という数字が現れたからというのがもう一つの理由です。
あとで説明しますが、1729 という数字は数学者にとって特別な数字なのです。
現在のところ実用的な応用は限られますが、理論的な影響は途方もなく大きいと言われています。というのも乗算はあらゆる数学的な操作の中心にあるものだからです。なので、その速度は計算複雑性理論においては、 物理学における光速に匹敵するほど重要なわけです。
かけ算が O(n log n) ステップで実行できることは示されましたが、これよりも速いアルゴリズムが存在しないことは (多くの人はそう考えていますが) 今のところまだ証明されていません。
1729 の話
時は第一次大戦前夜、インドに Srinivasa Ramanujan という青年がいました。彼は数学の専門的な教育は受けておらず、独学で数学の研究に没頭していました。周りのすすめもあって、研究成果を宗主国であるイギリスの数学の教授達に送ったのですが、 狂人の戯言だと黙殺される始末。そんな中、ただ一人 GodfreyHarold Hardy だけが Ramanujan の才能を見抜いて彼をケンブリッジ大学へ招聘します。Ramanujan は数学を専門的に学んでいないからか証明の必要性が理解できなかったそうです。そこでHardy は Ramanujan が朝持ってくる成果を一日かけて証明するというような研究スタイルを取り、その結果、大きな成果を得ました。
しかし、Ramanujan は敬虔なヒンドゥー教徒で厳格なベジタリアンだったこともあり、イギリスの生活が合わず次第に衰弱していきます。最終的にインドに帰国するもののまもなく1920年に亡くなってしまいました。
Ramanujan は本当の天才でした。彼がどれだけ並外れていたのか説明することは難しいですが、彼の考えた式をいくつか紹介します。
最初の式は恒等式です。
とんでもない数の項が出てくる式なのですが、それが右辺できれいに二乗の形にまとまっています。Hardy と Ramanujan はこの式を使って右辺が常に正または 0 であることから重要な不等式を証明しています。
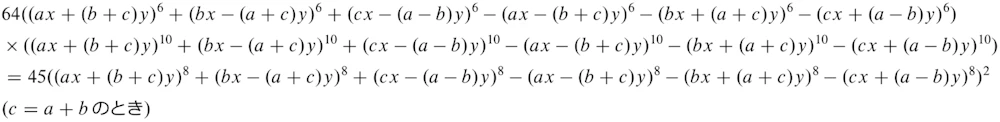
続いてはインドの不思議な旋律と呼ばれる公式です。
左側は連分数と言って、ある数を分数で次々と近似していく時に出てくる式です。これが右辺のような形にまとまるとはただただ驚くしかありません。
何故こんな式が考えだせるのかわかりませんが、この式もちゃんと成り立っています。
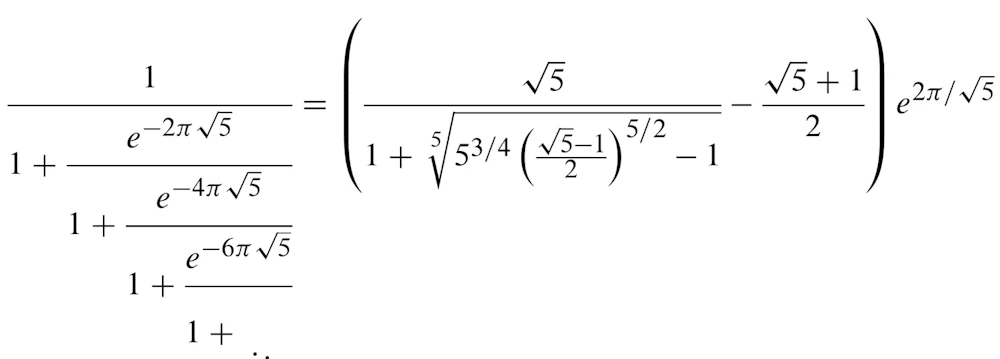
それでは 1729 の話をします。
ある日、療養所に入院していた Ramanujan を Hardy が見舞いに訪れました。その時に「乗ってきたタクシーのナンバーが 1729 だったが、特に特徴のない数だったよ」という話を Hardy が話したことに端を発します。
これに対して Ramanujan は「いえ 先生。1729 はとても興味深い数です。それは二つの整数の 3 乗の和として二通りに表すことができる最小の自然数です」というのをたちどころに返したそうです。
式にするとこういうことです。
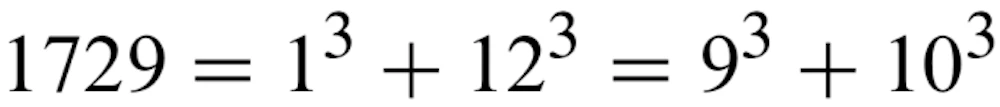
このエピソードから 1729 は数学者に「タクシー数」として親しまれるようになりました。
今日の話の参考文献を紹介しておきますので、興味のある方は読んでみてください。Ramanujan については映画にもなっているのでよかったら見てみてください。
参考文献
Klarreich, E.Multiplication hits the speed limit.
DOl:https://doi.org/10.1145/3371387
Harvey, D. and van der Hoeven, J.
Integer Multiplication in Time O(n log n).
Knuth, D.E.
The Art of Computer Programming, vol. 2: Seminumerical Algorithms, 3rd edn, Addison-Wesley, 1998, 294-318.
映画「奇蹟がくれた数式」(The Man Who Knew Infinity)

S2ファクトリー株式会社
様々な分野のスペシャリストが集まり、Webサイトやスマートフォンアプリの企画・設計から制作、システム開発、インフラ構築・運用などの業務を行っているウェブ制作会社です。
実績
案件のご依頼、ご相談、その他ご質問はこちらからお問い合わせください。






