2020/06/11
最近のコンパイラの最適化技法

暑くなってきて夏バテ気味です。
家に引きこもっているせいで余計に体力が落ちています。
強くなりたい。
今回は弊社の荒川が「最近のコンパイラの最適化技法」ということで、Communications of the ACM の記事『Optimizations in C++ compilers』を紹介したのですが、かなり長い発表だったため簡略化しました。ご了承ください。
興味の湧いた方はリンクから記事に飛んで購入し、実際に読んでみていただけますと幸いです。
Communications of the ACM に載った『Optimizations in C++ compilers』という記事について紹介です。
10年間ゲームの開発会社で、スプライト、爆発、複雑な背景などを作り込む仕事をしていました。アセンブリ言語を使ってカスタマイズをやったり、コンパイラの出力を読んでその能力を確認したり、複雑かつ緻密な業務に従事していたそうです。
その後トレーディング会社に転職。
これまで扱ってきたスプライトやポリゴンから、財務データを扱う仕事に変わりましたが、コンパイラの仕組みについて理解していたおかげで順応できたとのこと。
そして2012年、会社で新しい C++11 の機能のうちどれを採用するかを議論していたらしく、その時重要視されたのは、ナノ秒単位で数えるような場合、性能を犠牲にしないコードの書き方を決めておくことだったそう。
auto、lambda、範囲ベース for 文などの新しい機能を試すために、下の図のような shell script で常にアセンブリ出力を行うようにしたらしいです。
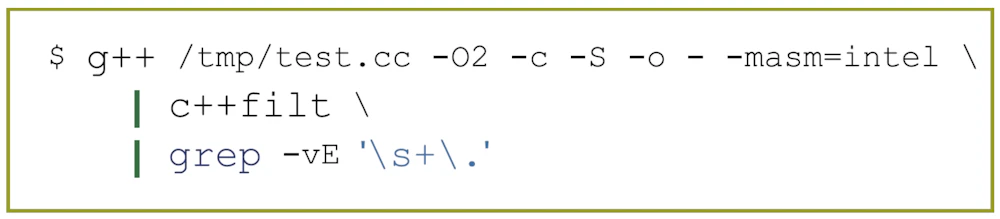
この仕組みは「こうしたらどうなる?」に対処するのに非常に効果的だったので、これを応用して CompilerExplorer が作られました。
コンパイラが行っていることを理解するのは大切なので、プログラミング言語のユーザーは少しだけアセンブリ言語を学ぶことを著者は推奨しています。
ちなみに、この記事中で例に挙げてあるアセンブリ言語は 、64 ビット x86 プロセッサのものです。
また、コンパイラとして GCC と Clang のみを挙げていますが、Microsoft や Intel のものも同様に賢い最適化を行っているそうです。
それでは最適化について見ていきましょう。
多くの最適化は “strength reduction” (演算子強度低減) という範疇に入り、
“strength reduction”とは、高価な (重い) 処理を対象に、それをより軽い処理に変換することをいいます。
簡単な礼を使って説明します。
ループ内に乗算がある場合です。

乗算は加算より遅いので、コンパイラはこれを下のように加算して、その結果を直接出すように書き換えます。

こうすることで乗算の重い処理がなくなり、計算スピードが速くなります。
これが最適化の基本となります。
Inlining (インライン化)
Constant folding (定数のたたみ込み)
Constant propagation (定数の伝播)
Common subexpression elimination (共通部分式除去)
Dead code removal (デッドコード削除)
Instruction selection (命令の選択)
これらが最適化のカテゴリーです。
大原則としては、可能な限り多くの情報をコンパイラに渡すことが、正しい最適化につながるということです。
もちろん多くの情報を渡せば、それだけコンパイルに時間が掛かるようになるので、バランスを考慮する必要があります。
ここまで最適化の概念的な部分をざっと説明しましたが、次からはコンパイラを使った具体的な例を見ていきます。
足し算の50倍の時間がががり、掛け算のさらに10倍の時間がかかります。
なので割り算を使わないようにしたい。
例えばこれはプログラマーがよくやるテクニックですが、 2 の冪乗で割る時は割り算を使わずにシフト演算で置き換える方法があります。
しかし実はこの場合でも、置き換えはコンパイラに任せて素直に割り算を使った方が負の数で間違わずに済みます。
では、割る数が 2 の冪乗でなかった場合はどうなるのか。
このようなコードがあるとします。

これをコンパイラにかけると、下のように出力されます。

割り算はなくなり、代わりに奇妙な 32ビットの値 0xaaaaaaab との掛け算と 64
ビット値の 33 ビットの右シフトが使われています。
これは何をしているのかというと、コンパイラは割り算をより安価な逆数の掛け算に変換しているのです。
逆数として、固定小数点での値 (十進数に直すと 0.33333333337213844) を使い、結果から固定小数点分の 33 ビットをシフトしなおして、元の値としています。
コンパイラはこのように、適切な固定小数点と定数を決定するアルゴリズムを備えており、丸め誤差を含めて割り算と完全に同一の値が得られるようになっています。
定数の割り算についてコンパイラの機能はすごいということはわかりましたが、そもそも割り算をそんなに頻繁に使うのかという疑問があると思います。
割り算というよりは、ハッシュ値からハッシュテーブルのインデックスを求めるのに剰余演算 (%, modulus)が頻繁に使われるために重要なのです。
例えば、
下のコードは 1 になっているビットを数える関数の例です。

式中の a &(a - 1) はビット列の最も右側の 1 を 0 に変更する処理ですが、
最も右側の 1 をどんどん変換していった数がループした回数になるので、結果的に値の中で 1 になっているビットがいくつあったか調べられるということになります。
このコードをそれぞれのコンパイラにかけてみましょう。

命令選択の良い例であり Clang は完璧な命令を選んでいると言っていいでしょう。
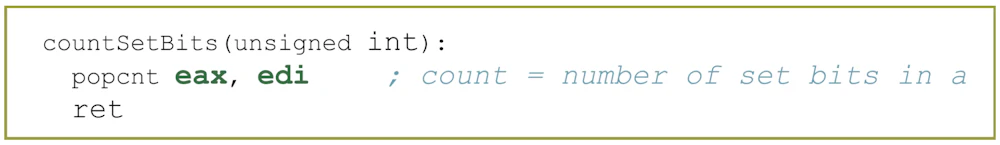
これは POPCNT では eax の以前の値に依存関係があると判断してしまう Intel CPU のバグを回避するために実行されているようです。

コンパイラは、今日ではほとんどの CPU が備えているベクトル化命令 (SIMD 命令) を非常にうまく利用してこれを処理します。
これは2 乗の和を計算するコードですが、

最適化すると、コンパイラは SIMD を使ったコードを出力し、
一度に 8 個ずつの値を 2 乗して、8 個それぞれの総和を計算してくれます。

昔はこれをいちいち自分で書いていたのですが、コンパイラの最適化のレベルを十分に上げて、適切な対象CPU アーキテクチャを指定するだけで、ベクトル化演算が呼び出され処理してくれるのです。
しかし一つ注意点がありまして、この処理は 8 個目毎の値の小計を求め、小計を足し合わせることで総合計を求めているので、プログラムで指定した通りの足す順番と一致していません。
整数の足し算の場合は順番を変えても影響はないのですが、浮動小数点では話が変わってきます。
浮動小数点では (a+b)+c は a+(b+c) と必ずしも一致しないということを頭に置いておいてください。
もしも足し算の順序が重要でないと確信が持てるならば 、GCC に危険なフラグ -funsafe-mathoptimizations を渡すと、素晴らしいコードを書き出してくれます。
著者がコンパイラの挙動について試しているうちにもっと面白いことに気がついたのが数列の総和でした。
これは 0 から x までの間を足して結果を返す単純なコードです。

GCC でコンパイルすると、とても素直なコードを出力し、ベクトル化もきちんと行って処理の速いコードを出してくれるのですが、 clang の場合だとちょっと変わったコードにコンパイルされます。

上のものは Clang が出したコードですが、まずループがありません。
Clang では、(x – 1)(x – 2)/2 + (x + 1) という値を返しているのですが、これは数列の総和の公式 x(x – 1)/2 そのものです。
この閉じた形がいつも処理が少ないとは限らないのですが、Clang のみが、この種のループの閉じた形への変換を行います。
ループの処理結果は、途中で値がオーバーフローしてしまう場合は、総和の公式とは一致しません。
しかし signed integer のオーバーフローは undefied behavior (未定義の動作) なので、この不一致は問題にならないのです。
参考文献
Warren, H.S. Hacker’s Delight. 2nd edition. Addison-Wesley Professional, 2012.
家に引きこもっているせいで余計に体力が落ちています。
強くなりたい。
今回は弊社の荒川が「最近のコンパイラの最適化技法」ということで、Communications of the ACM の記事『Optimizations in C++ compilers』を紹介したのですが、かなり長い発表だったため簡略化しました。ご了承ください。
興味の湧いた方はリンクから記事に飛んで購入し、実際に読んでみていただけますと幸いです。
Communications of the ACM に載った『Optimizations in C++ compilers』という記事について紹介です。
この記事について
著者はMatt Godbolt。10年間ゲームの開発会社で、スプライト、爆発、複雑な背景などを作り込む仕事をしていました。アセンブリ言語を使ってカスタマイズをやったり、コンパイラの出力を読んでその能力を確認したり、複雑かつ緻密な業務に従事していたそうです。
その後トレーディング会社に転職。
これまで扱ってきたスプライトやポリゴンから、財務データを扱う仕事に変わりましたが、コンパイラの仕組みについて理解していたおかげで順応できたとのこと。
アセンブリ言語
コンピュータなどのプログラミング言語の1種で、原則として機械語の命令命令に1対1で対応した、人間に理解しやすい文字列や記号で記述される。 いわゆる高水準言語に対して低水準言語と分類される。
コンパイラ
コンピュータの自動プログラミングに使うプログラムの一種。一般に、一定方式に従い、使用機種には依存せず人間に分かりよい形で書いたプログラムを、機械コード(=機械がすぐ実行できる形)に翻訳する仕事を受け持つ。また「コンパイラ言語(=コンパイラに与えるために約束された人工言語)」の略語としても使う。
そして2012年、会社で新しい C++11 の機能のうちどれを採用するかを議論していたらしく、その時重要視されたのは、ナノ秒単位で数えるような場合、性能を犠牲にしないコードの書き方を決めておくことだったそう。
auto、lambda、範囲ベース for 文などの新しい機能を試すために、下の図のような shell script で常にアセンブリ出力を行うようにしたらしいです。
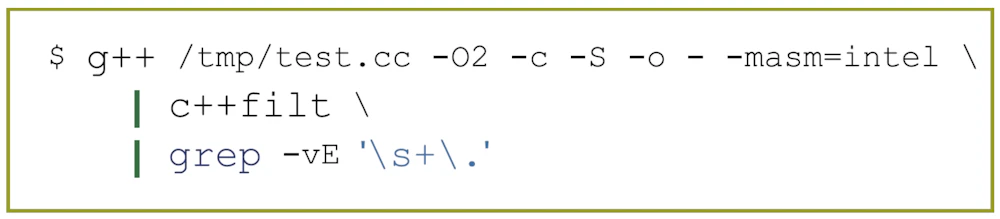
この仕組みは「こうしたらどうなる?」に対処するのに非常に効果的だったので、これを応用して CompilerExplorer が作られました。
コンパイラが行っていることを理解するのは大切なので、プログラミング言語のユーザーは少しだけアセンブリ言語を学ぶことを著者は推奨しています。
ちなみに、この記事中で例に挙げてあるアセンブリ言語は 、64 ビット x86 プロセッサのものです。
また、コンパイラとして GCC と Clang のみを挙げていますが、Microsoft や Intel のものも同様に賢い最適化を行っているそうです。
それでは最適化について見ていきましょう。
最適化の初級コース
最適化について学ぶ前に、コンパイラが使ういくつかの概念を知っておくことは大切です。多くの最適化は “strength reduction” (演算子強度低減) という範疇に入り、
“strength reduction”とは、高価な (重い) 処理を対象に、それをより軽い処理に変換することをいいます。
簡単な礼を使って説明します。
ループ内に乗算がある場合です。

乗算は加算より遅いので、コンパイラはこれを下のように加算して、その結果を直接出すように書き換えます。

こうすることで乗算の重い処理がなくなり、計算スピードが速くなります。
これが最適化の基本となります。
最適化のカテゴリー
先ほどの例は“strength reduction”でしたが、他にも色々なカテゴリーがあるので、それらについても簡単に説明しておきます。Inlining (インライン化)
- 関数呼び出しを関数の実体で置き換える
- これによってさらに最適化が可能になる
Constant folding (定数のたたみ込み)
- コンパイル時に値が計算できる場合は、式をその結果で置き換える
Constant propagation (定数の伝播)
- 変数を追跡して値が変化しない場合は、その定数で置き換える
Common subexpression elimination (共通部分式除去)
- 重複した計算がある場合は、一度だけ計算して結果をコピーする
Dead code removal (デッドコード削除)
- 他の多くの最適化を行った後では、出力に影響しないコードを除去できる
- 使われない値のロードやストア、使われない関数、式
Instruction selection (命令の選択)
- いわゆる最適化とは異なるが、コンパイラがプログラムの内部表現を CPUの命令に変換する際、等価な命令列が数多くある
- それらの中から正しい選択をするためには対象となるプロセッサのアーテクチャについて多くのことを知っておく必要がある
これらが最適化のカテゴリーです。
大原則としては、可能な限り多くの情報をコンパイラに渡すことが、正しい最適化につながるということです。
もちろん多くの情報を渡せば、それだけコンパイルに時間が掛かるようになるので、バランスを考慮する必要があります。
ここまで最適化の概念的な部分をざっと説明しましたが、次からはコンパイラを使った具体的な例を見ていきます。
定数の割り算
近代的なCPUで一番重い演算は整数の割り算です。足し算の50倍の時間がががり、掛け算のさらに10倍の時間がかかります。
なので割り算を使わないようにしたい。
例えばこれはプログラマーがよくやるテクニックですが、 2 の冪乗で割る時は割り算を使わずにシフト演算で置き換える方法があります。
しかし実はこの場合でも、置き換えはコンパイラに任せて素直に割り算を使った方が負の数で間違わずに済みます。
では、割る数が 2 の冪乗でなかった場合はどうなるのか。
このようなコードがあるとします。

これをコンパイラにかけると、下のように出力されます。

割り算はなくなり、代わりに奇妙な 32ビットの値 0xaaaaaaab との掛け算と 64
ビット値の 33 ビットの右シフトが使われています。
これは何をしているのかというと、コンパイラは割り算をより安価な逆数の掛け算に変換しているのです。
逆数として、固定小数点での値 (十進数に直すと 0.33333333337213844) を使い、結果から固定小数点分の 33 ビットをシフトしなおして、元の値としています。
コンパイラはこのように、適切な固定小数点と定数を決定するアルゴリズムを備えており、丸め誤差を含めて割り算と完全に同一の値が得られるようになっています。
定数の割り算についてコンパイラの機能はすごいということはわかりましたが、そもそも割り算をそんなに頻繁に使うのかという疑問があると思います。
割り算というよりは、ハッシュ値からハッシュテーブルのインデックスを求めるのに剰余演算 (%, modulus)が頻繁に使われるために重要なのです。
1 になっているビットを数える
このような機会はほとんどないと思われるかもしれないですが、この単純な演算が意外といろんな場面で役に立ちます。例えば、
- 二つのビット列の Hamming 距離を計算する
- 疎行列の圧縮表現を扱う場合
- ベクトル演算の結果を処理する場合
下のコードは 1 になっているビットを数える関数の例です。

式中の a &(a - 1) はビット列の最も右側の 1 を 0 に変更する処理ですが、
最も右側の 1 をどんどん変換していった数がループした回数になるので、結果的に値の中で 1 になっているビットがいくつあったか調べられるということになります。
このコードをそれぞれのコンパイラにかけてみましょう。
GCC 8.3 の場合
GCC は a &(a - 1) を一番右の 1 を 0 に変える操作だと認識して、ビット操作専用命令BLSR を発行しています。
Clang 7.0 の場合
この関数がビットを数える処理だと認識して、関数全体を一命令の POPCNT (population count)に置き換えています。命令選択の良い例であり Clang は完璧な命令を選んでいると言っていいでしょう。
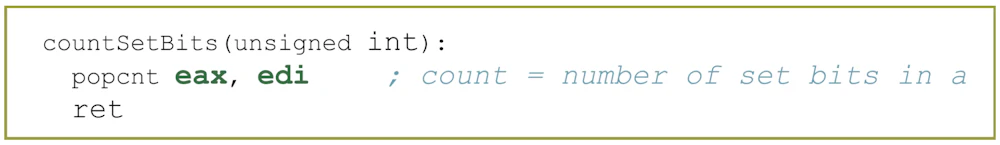
GCC 9 の場合
GCC 9 も Clang 7.0 と同じようなコードを生成するのですが、直後に上書きされる eax レジスタをわざわざ 0 クリアしています。これは POPCNT では eax の以前の値に依存関係があると判断してしまう Intel CPU のバグを回避するために実行されているようです。

2 乗の和の計算
時として何かを足し合わせる処理が必要になることがありますが、コンパイラは、今日ではほとんどの CPU が備えているベクトル化命令 (SIMD 命令) を非常にうまく利用してこれを処理します。
これは2 乗の和を計算するコードですが、

最適化すると、コンパイラは SIMD を使ったコードを出力し、
一度に 8 個ずつの値を 2 乗して、8 個それぞれの総和を計算してくれます。

昔はこれをいちいち自分で書いていたのですが、コンパイラの最適化のレベルを十分に上げて、適切な対象CPU アーキテクチャを指定するだけで、ベクトル化演算が呼び出され処理してくれるのです。
しかし一つ注意点がありまして、この処理は 8 個目毎の値の小計を求め、小計を足し合わせることで総合計を求めているので、プログラムで指定した通りの足す順番と一致していません。
整数の足し算の場合は順番を変えても影響はないのですが、浮動小数点では話が変わってきます。
浮動小数点では (a+b)+c は a+(b+c) と必ずしも一致しないということを頭に置いておいてください。
もしも足し算の順序が重要でないと確信が持てるならば 、GCC に危険なフラグ -funsafe-mathoptimizations を渡すと、素晴らしいコードを書き出してくれます。
数列の総和
最後の例です。著者がコンパイラの挙動について試しているうちにもっと面白いことに気がついたのが数列の総和でした。
これは 0 から x までの間を足して結果を返す単純なコードです。

GCC でコンパイルすると、とても素直なコードを出力し、ベクトル化もきちんと行って処理の速いコードを出してくれるのですが、 clang の場合だとちょっと変わったコードにコンパイルされます。

上のものは Clang が出したコードですが、まずループがありません。
Clang では、(x – 1)(x – 2)/2 + (x + 1) という値を返しているのですが、これは数列の総和の公式 x(x – 1)/2 そのものです。
この閉じた形がいつも処理が少ないとは限らないのですが、Clang のみが、この種のループの閉じた形への変換を行います。
ループの処理結果は、途中で値がオーバーフローしてしまう場合は、総和の公式とは一致しません。
しかし signed integer のオーバーフローは undefied behavior (未定義の動作) なので、この不一致は問題にならないのです。
参考文献
Warren, H.S. Hacker’s Delight. 2nd edition. Addison-Wesley Professional, 2012.

S2ファクトリー株式会社
様々な分野のスペシャリストが集まり、Webサイトやスマートフォンアプリの企画・設計から制作、システム開発、インフラ構築・運用などの業務を行っているウェブ制作会社です。
実績
案件のご依頼、ご相談、その他ご質問はこちらからお問い合わせください。